Welcome to Jazz Audio-Aligned Harmony (JAAH) Dataset’s documentation!

Dataset statistics

Contains 113 tracks
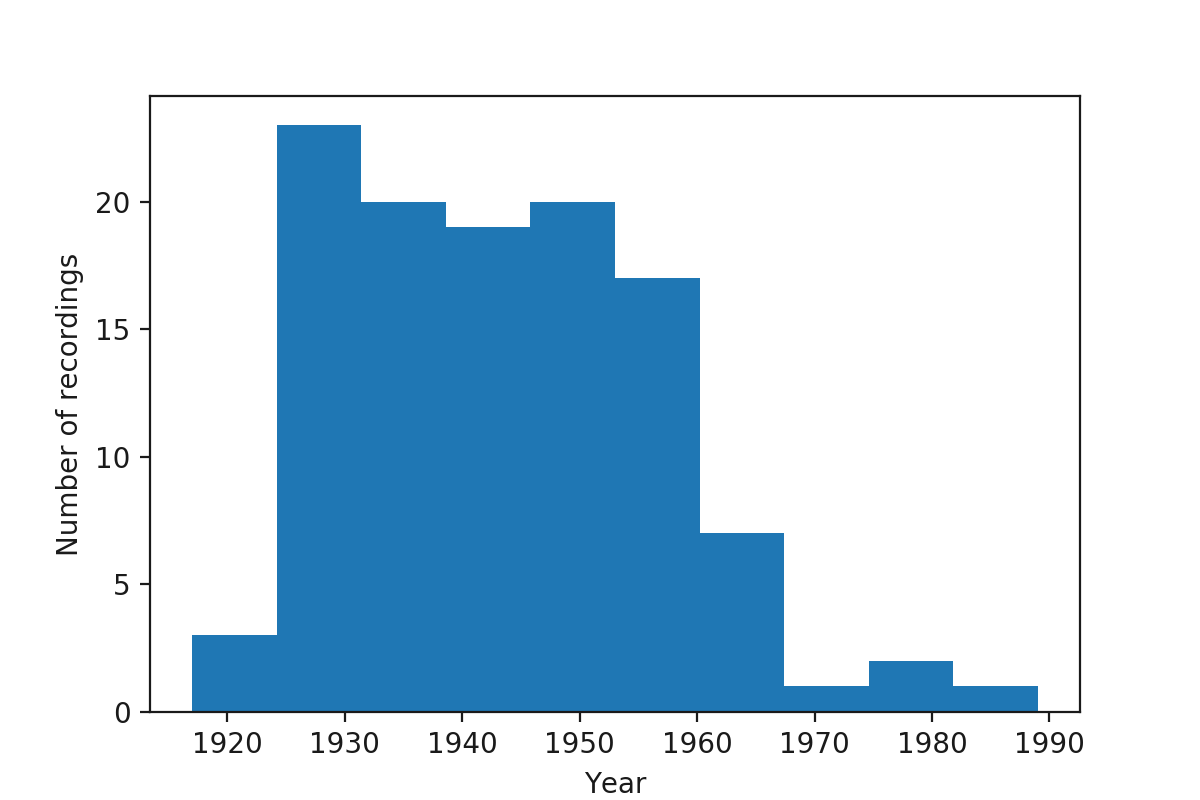
Time period 1917 - 1989
Number of Chord Segments 17600
Mean BPM 164.560654012
Mean Harmonic Rhythm 3.6651136363636363
Chord Usage Summary
Chord Beats Number Beats % Duration (seconds) Duration %
maj 18591 27.1124398425 6606.114 26.4232764649
min 13172 19.209566866 4680.954 18.7229802062
dom 29786 43.4388216421 10557.523 42.2282069328
hdim7 1280 1.86670555637 511.15 2.04450873313
dim 1677 2.44567595158 582.86 2.33133592916
N 3986 5.81303777162 2032.415 8.12929710818
unclassified 78 0.113752369841 30.1 0.120394625584

Histogram by year

_images/index-1.png

Top Bigrams

(see Bigram in glossary)

_images/index-2.png

Top N-grams

(see N-gram in glossary)

_images/index-3.png

Contents

Glossary

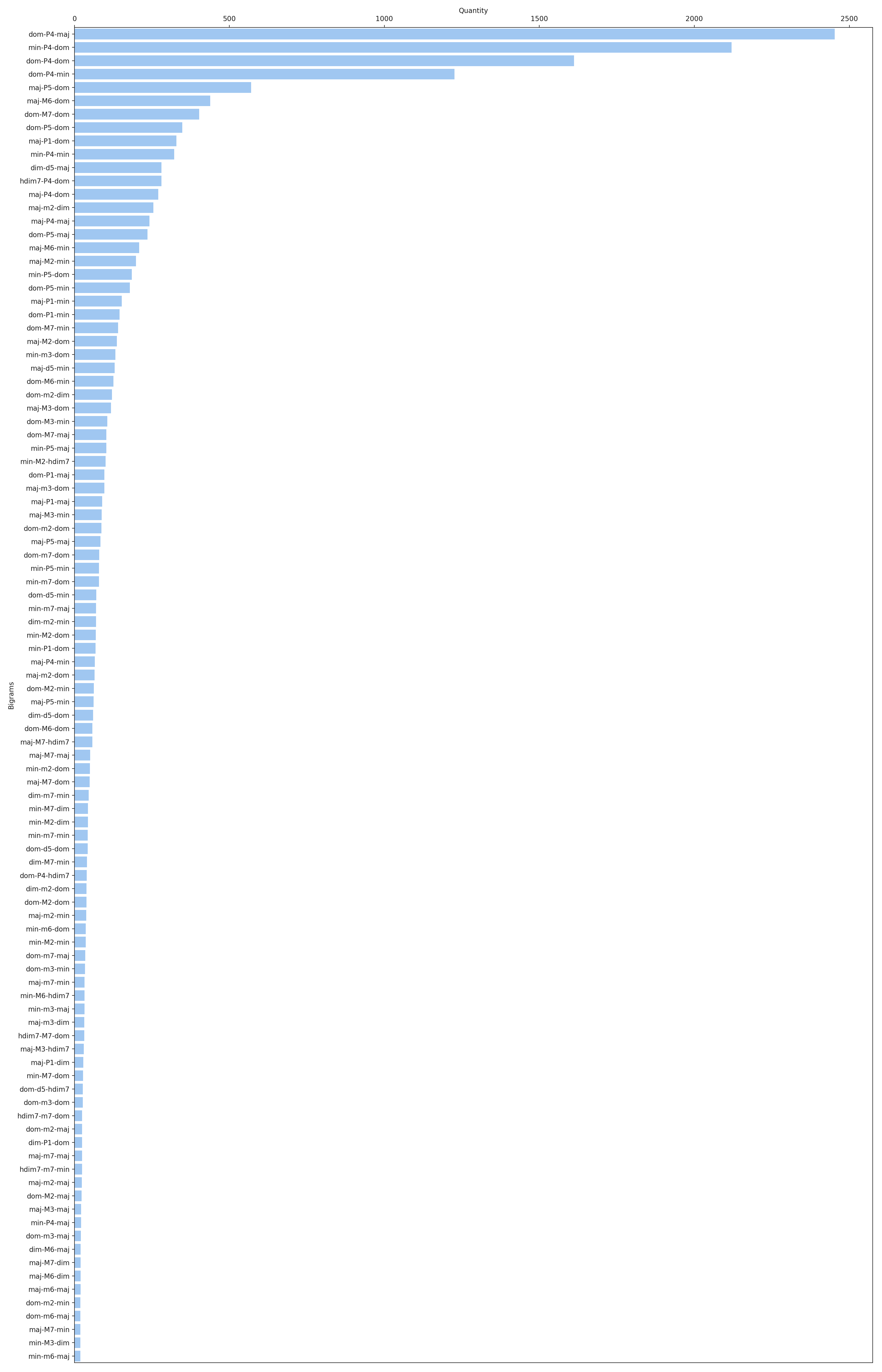
Bigram

Bigram represents chords transition event. “Absolute” chord pitches are omitted, bigram is denoted by:

  • first chord quality (i.e. Maj, Min, Dom, HDim7, Dim)

  • interval between first and second chord roots encoded by:

    • Letter: Perfect, Major or minor
    • number (2 for second, 3 for third, etc)

  • second chord quality

The approach is taken from [BS13].

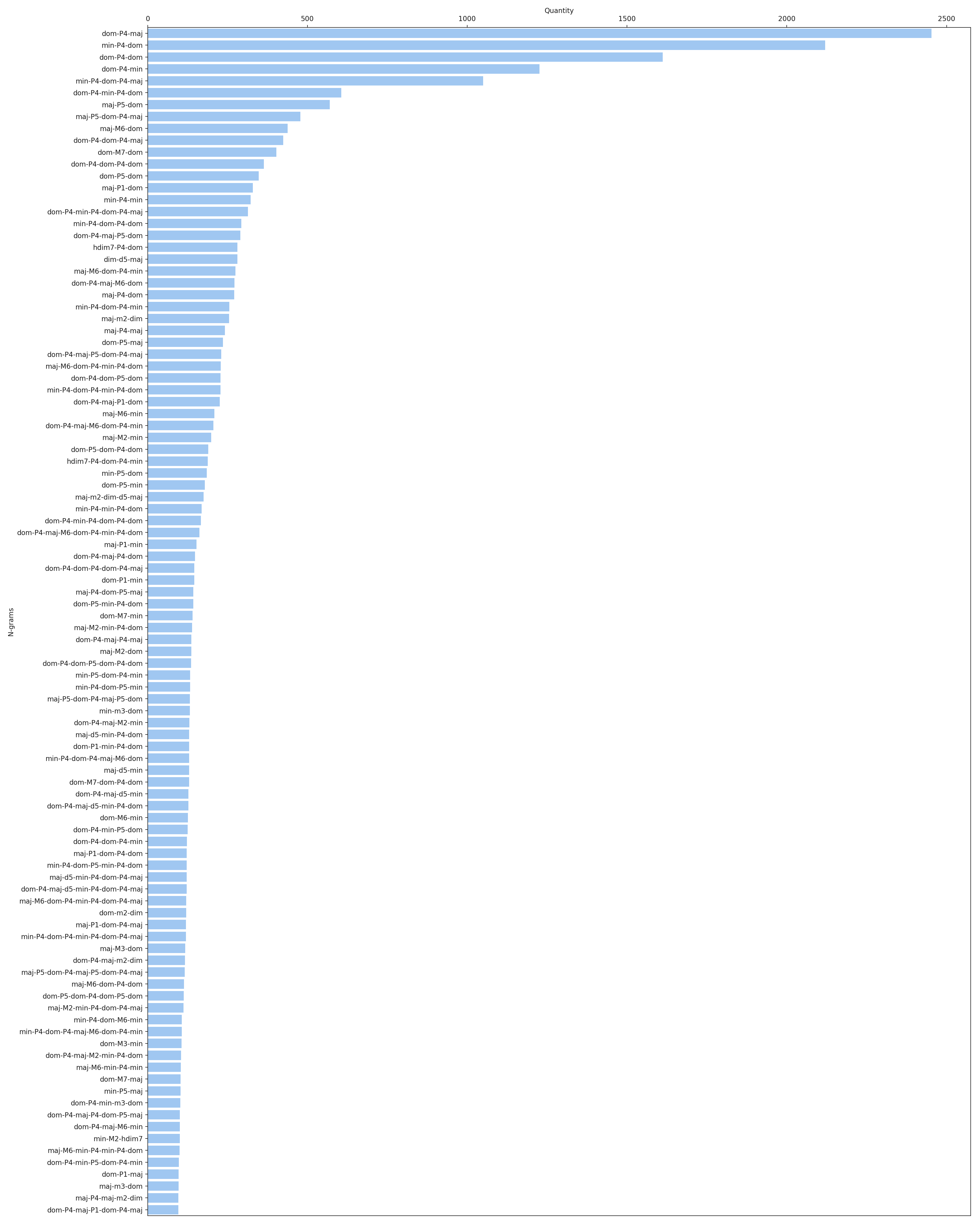
N-gram
Represent sequence of chord transition events. “Absolute” chord pitches are omitted, only chord qualities and inter-root intervals are considered (see Bigram).
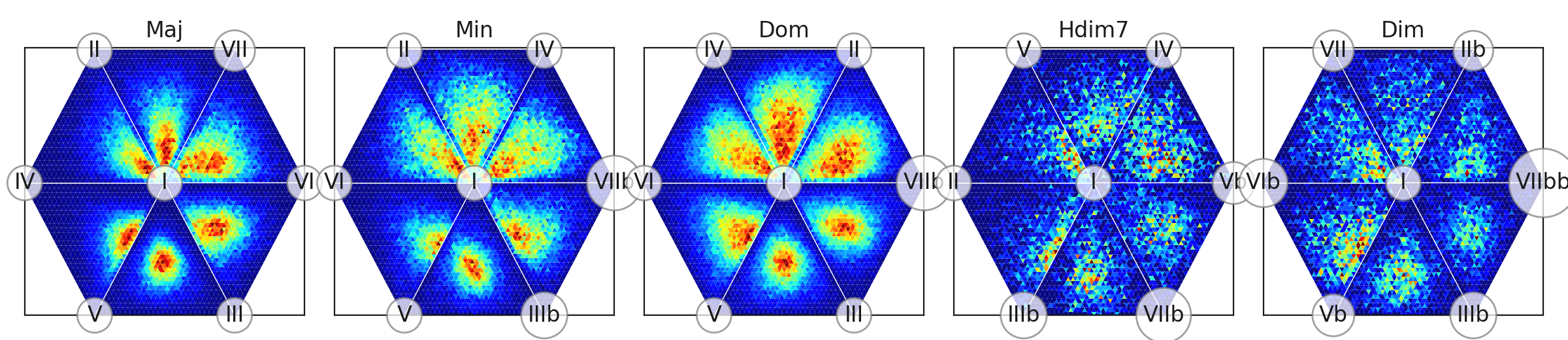
Chord type chroma distribution ternary plot

Lead sheet chord chart is the backbone of performance in many jazz styles. But each performance and style has it’s own “sonic aura” determined by how conceived chords are realized by musicians. The main idea of these plots is to provide visual profiles for each of main chord types used in jazz (major, minor, dominant seventh, halfdiminished seventh and diminished) for the whole dataset and for each track. Chroma distribution plots show:

  • What degrees (relative to a chord’s root) are actually presented, and quantitative measurement of their presence.
  • Joint distribution of the degrees (it shows e.g. how often certain degrees are played together or are they used independently)
  • Dispersion of degree usage

How are they produced?

  1. NNLS Chroma features (http://www.isophonics.net/nnls-chroma , [MD10]) are extracted for each frame of audio recordings. Each chroma is a 12-dimensional vector, with components representing 12 semitone pitch classes.
  1. Pitch-class based chroma converted to degree-based chroma. I.e. chroma vectors corresponding to each particular chord are transposed to the common root, so the new vector’s first component represents intensity of chord root pitch, the following - intensity of minor second, etc.
  1. For each beat, “beat predominant chroma” is calculated. This is a single 12d vector which represents predominant chroma around this beat. To estimate it, we convolve per-frame chroma vectors with Hanning window (https://en.wikipedia.org/wiki/Hann_function) and then use vectors corresponding to beat frames. Thus, maximum weights are given to frames, close to the beat and weights are decreased as frames are moving away from the beat.
  1. We rather interested in proportion of chroma components in a certain sound segment, but not in it’s absolute values, so we normalize them with \(l1\) norm. So they are sum up to one (and they are non-negative by definition).
  2. Normalized chroma vectors don’t fill the whole 12D space. They are distributed on standard 11-simplex (https://en.wikipedia.org/wiki/Simplex): \(\{x\in \mathbb {R} ^{12}:x_{0}+\dots +x_{11}=1,x_{i}\geq 0,i=0,\dots ,11\}\). To visualize it’s distribution we borrow techniques from Compositional Data Analysis (e.g. [vdBTD13]). Such techniques are used when proportions of parts is explored (e.g. chemical composition or budget composition). Our 11-d simplex has 12 vertices corresponding to 12 semitones addressed as chord degrees. It’s confined by 220 triangle faces (each face corresponds to unique triple combination of the degrees, e.g. I-III-V). To see what’s inside, we produce two dimensional projections of the simplex content to it’s faces, representing density with color. For each triple we marginalize out chroma components which are not inculded in the triple and obtain distribution of 3 chord degrees which is defined on a triangle. Resulted figure is called Ternary plot (https://en.wikipedia.org/wiki/Ternary_plot). Out of 220 triangles, we show only six, related to the most “significant” chord degrees. (“Significance” here means that chroma components for these degrees have highest average values throughout the whole dataset), triangles are arranged into hexagons adjoined by identical edges for presentation simplicity.
Mean harmonic rhythm
Rate (in chords per beat) at which chords are changed. See e.g.: https://en.wikipedia.org/wiki/Harmonic_rhythm

References

[BS13]Yuri Broze and Daniel Shanahan. Diachronic Changes in Jazz Harmony: A Cognitive Perspective. Music Perception: An Interdisciplinary Journal, 3(1):32–45, 2013. URL: http://www.jstor.org/stable/10.1525/mp.2013.31.1.32 http://www.jstor.org/page/info/about/policies/terms.jsp, doi:10.1525/mp.2013.31.1.32.
[MD10]Matthias Mauch and Simon Dixon. Approximate note transcription for the improved identification of difficult chords. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), number 1, 135–140. 2010. URL: https://www.eecs.qmul.ac.uk/{~}simond/pub/2010/Mauch-Dixon-ISMIR-2010.pdf.
[vdBTD13]K. Gerald van den Boogaart and Raimon Tolosana-Delgado. Fundamental Concepts of Compositional Data Analysis. In Analyzing Compositional Data with R, pages 13–50. Springer Berlin Heidelberg, Berlin, Heidelberg, 2013. URL: http://link.springer.com/10.1007/978-3-642-36809-7{\_}2, doi:10.1007/978-3-642-36809-7_2.